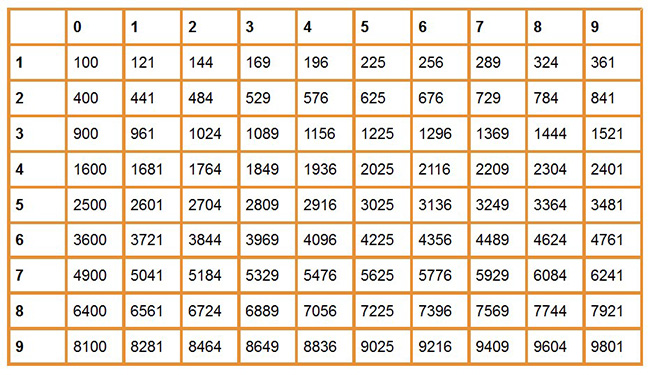
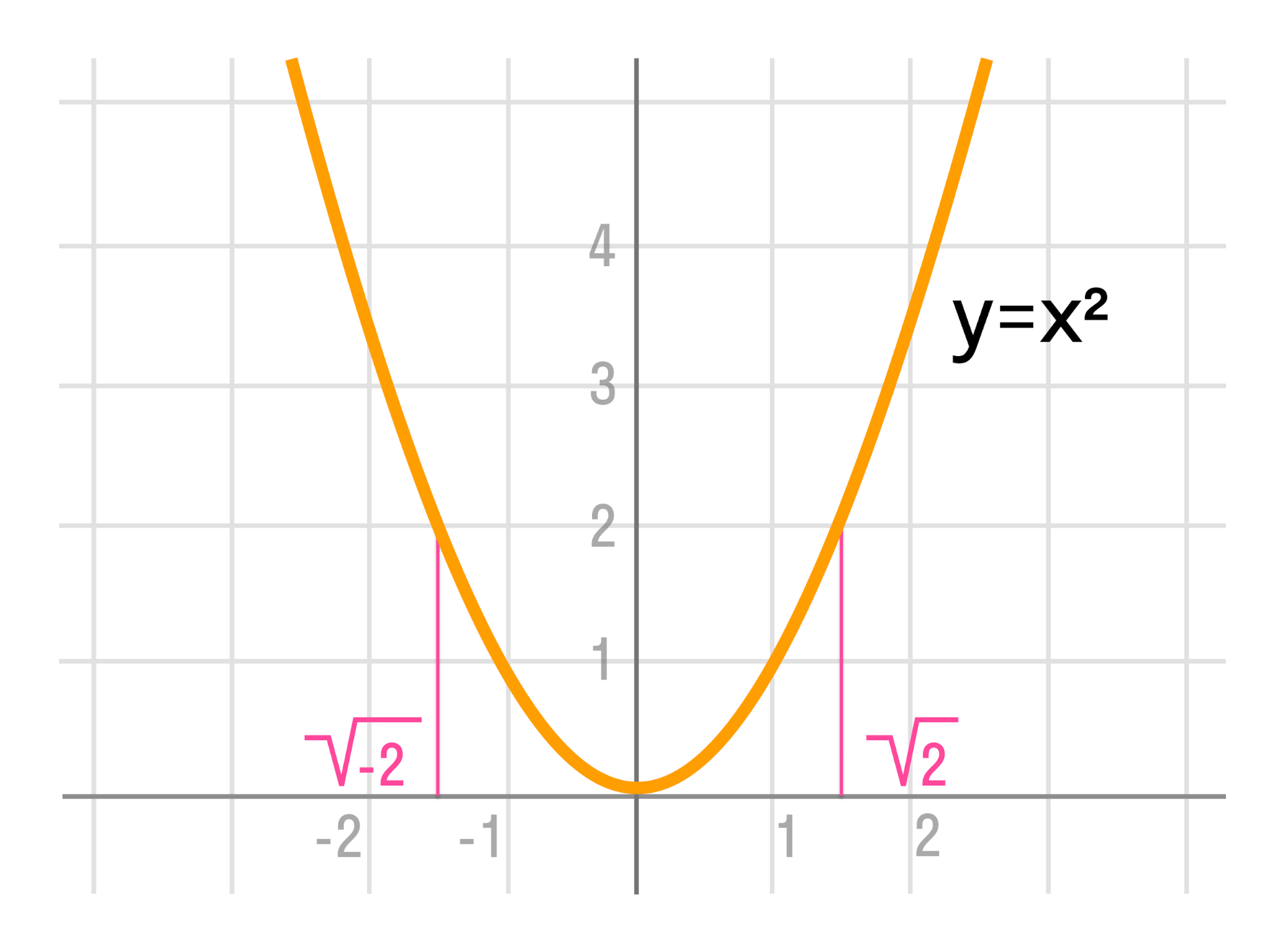
Что такое квадратный корень
Наличие квадратных корней в выражении усложняет процесс деления, однако существуют правила, с помощью которых работа с дробями становится значительно проще. Единственное, что необходимо все время держать в голове — подкоренные выражения делятся на подкоренные выражения, а множители на множители. В процессе деления квадратных корней мы упрощаем дробь.




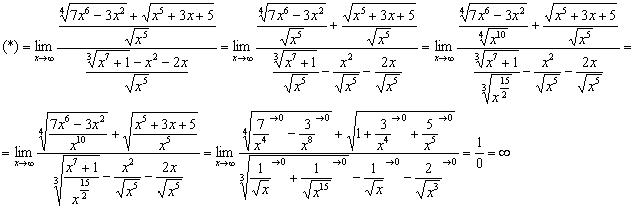
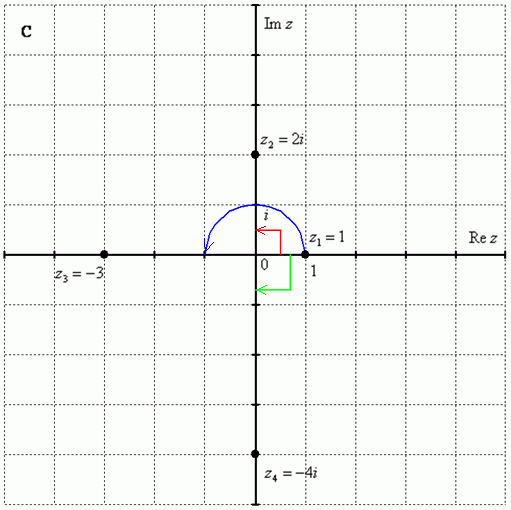

При возведении в квадрат что неотрицательного, что равного ему по модулю отрицательного числа, получается число неотрицательное. Поэтому операция извлечения квадратного корня из числа не является обратной к возведению числа в квадрат. Как в случае с обыкновенными дробями, так и с арифметическим квадратным корнем иногда можно сделать какие-то вычисления, а иногда нельзя. Представим подкоренное выражение в виде квадрата:. Выполним преобразование, используя формулу квадрата разности:.



Геометрически это означает построение стороны квадрата с заданной площадью. Любое положительное вещественное число имеет два корня [ 1 ]. Главное значение квадратного корня большинства положительных вещественных чисел является иррациональным числом с бесконечной последовательностью десятичных цифр. Как результат, десятичное представление любого такого квадратного корня может быть вычислено только приближённо с конечной точностью знаков после запятой.